It’s been a long time since I posted a blog – I retired from teaching Middle School in June, 2017, but have been subbing for one of the teachers at my old school for a few days. I decided I wanted to write about the progression in her algebra class using the Generic Rectangle because I think it is so amazing, and the topics just logically flow together so intuitively. Then I read my last post – and my algebra class had been using the Generic Rectangle! So some of this is also in my last post, but… it’s been a while, and I want to write about the whole thing. Maybe you will want to do it in your algebra classes!
When my friend began teaching her kids to multiply binomials, she used the Generic Rectangle. It’s called generic because the sizes of the boxes in the rectangle aren’t scaled to size, you just draw a rectangle and split it into 4 boxes. Before using the Generic Rectangle I would tell the kids to do the Double Distributive Property, but both of us didn’t say FOIL to our classes. This year her classes had a hashtag “#NOFOIL”. The book says FOIL.
Anyhow, she taught the kids to multiply binomials (or a monomial times a binomial, or binomial times trinomial) using the Generic Rectangle:

So now I’m subbing and it’s time to factor trinomials. The book has separated factoring into 2 sections: trinomials with a leading coefficient of 1, and trinomials with leading coefficients not 1. I decided to teach them together, since we’d be using the same procedure we used in multiplying – the Generic Rectangle.
To start the day we did a warm up/review of “Diamond Problems” – since most of the kids had used the CPM books last year and had done lots of these problems. I usually call it the “X” (because I’m too lazy to make a diamond around the X). They were quick to remember they’re looking for 2 numbers that will multiply to the top number, and add to the bottom number:

We also did a quick review of multiplying to remember where we put the terms on the outside of the rectangle, and how we get the terms in the trinomial.
Then I had them look at the rectangles again, and notice something about the products of the diagonals:

(Is this a coincidence? Nope. If you have a b c d outside the rectangle and multiply to get the inside boxes, then multiply the diagonals, you end up with abcd as both products.)
Now we could start factoring. I wrote down the problems, and had the kids tell me where to put the first and last terms in the Generic Rectangle. Then I drew an X and asked them what would go in the top… and they knew they could multiply the diagonal terms they had since it would be the same product as the diagonal terms they were looking for. Then I asked what term should be in the bottom of the X and they told me the middle term of my trinomial, since this is the sum of the diagonal terms they’re missing:

They then figured out that little puzzle, what multiplied to the top and added to the bottom terms, and filled in their Generic Rectangle. Now it was time to “undo” the rectangle! This is the most fun because it’s a little logic problem.
We begin by pulling out the GCF of 2 of the terms, either horizontally or vertically, their choice. This example shows me doing it vertically:
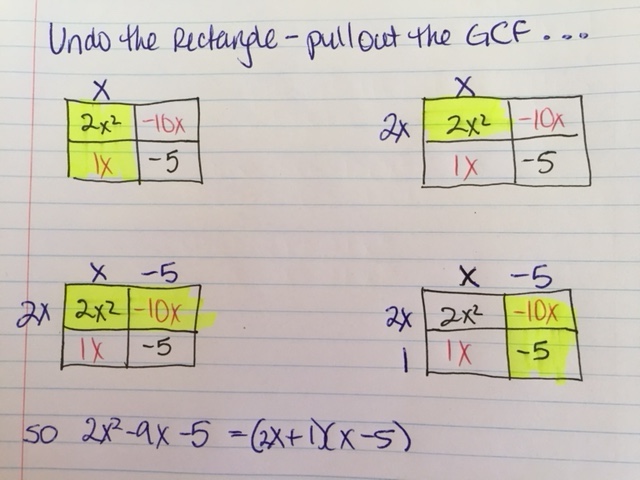
Here’s my thinking I did aloud with the class’s input (I didn’t draw different boxes):
Box on Upper Left: What is the largest term we can pull out of 2x^2 and 1x? x. Since we are doing the vertical terms, put the x on top of this column.
Box on Upper Right: What would I have multiplied x by to get 2x^2? 2x. So I write it outside, to the left.
Box on Lower Left: Now what would I multiply 2x by to get -10x? -5. Put this in the upper right space.
Box on Lower Right: Ok, what do I multiply -5 by to get -5? 1. This goes under the 2x, on the left.
So what are your factors? (2x+1)(x-5)! It’s so intuitive, the kids are good at thinking about these little puzzles, and they’re just undoing what the had been doing to multiply. We did about 8 problems in class, some with leading coefficients not 1, some with leading coefficients of 1, and the factoring was NO BIG DEAL. They didn’t have to do something different, or another step when the leading coefficient was not 1.
NOTE: We did factor out any GCF of the trinomial before doing the generic rectangle, and factor out a -1 if the leading coefficient was negative, and this resulted in a little confusion because some kids factored out the GCF then used the original trinomial terms in the Generic Rectangle. But that made for a good discussion, and helped with clarification. I think this is normal, some kids are just working and not really paying attention, so their “errors that happened because they really weren’t paying attention” help the class have a better understanding. Another result that helped with understanding was when a student wrote a fractional term outside of the Generic Rectangle – we multiplied out their factors and the integer factors and got the same trinomial. I asked them to just use integers for their factors. A couple of students had trouble factoring because they were taking the GCF of the “column” and writing it next to the “row” rather than on top of the “column”. So we did an example of that which was helpful. We also had a couple of students not copy the problem correctly from their trinomial into their rectangle…so it wouldn’t factor…but once they saw that they’d copied it wrong it wasn’t the Generic Rectangle’s fault anymore.
The following week I was back and it was time for Factoring By Grouping. They had a Trimester Test the first day I was there, and I was thinking about the lesson. It hit me that we should be able to use the Generic Rectangle to factor 4 terms (I don’t remembered if I taught this last year using the CPM Algebra book, I think we just had 4 terms and didn’t even worry about Factoring By Grouping) so decided to try it using the book’s examples. I drew the rectangle and filled in the terms, top row then bottom row, the same order as listed in the example. This worked great if there was only one variable, but the order of the problem in the book didn’t work when there were 2 variables. So I thought about it and rearranged the terms – which I did sometimes when Factoring By Grouping – and the Generic Rectangle worked great!
Class started and this is what we did:

Boom. They’re done. “Why was it even an issue? It’s the same thing!”, said the kids. “Yeah, I know, but the book has it as a separate section, because it’s not using the Generic Rectangle”, I said. “So… let’s do Factoring By Grouping, because some of you might like to do it instead, and I want you to know what it looks like.”
In my mind, the problem with Factoring By Grouping is that it is not intuitive. It doesn’t flow for the kids, because of FOIL. We are having the kids multiply in their heads, so they don’t see the second step. These are typical questions I would get when I’d taught it as another procedure to do, in the past:

When I learned how to factor we did the double distributive property to start, and wrote out the numbers we’d be multiplying. Actually that’s complete BS, I have no idea how I originally learned it. I do know we used Guess and Check to factor, and some problem were so annoying because the A and C terms had too many factor choices. But if we HAD written out the second step instead of doing it in our heads, then Factoring By Grouping would make sense. Here’s how I showed it to the kids – by doing the Double Distributive Property to multiply the factors, then showing Factoring By Grouping and highlighting the lines that are the same in both. The first example without the highlighting is just showing Factoring By Grouping and my thoughts on why it’s confusing:

We did some problems with 2 variables so they would see that they needed to think about the placement in the rectangle. It was great, in both classes the kids put the terms into the rectangle the same way I had done when I was looking at it. And we couldn’t factor it. So I asked another way we could arrange the terms and then we got it. I told them sometimes they’d have to think about where to put the terms. They would put in one term, factor it, and then figure out what other term would have that factor. They’d write that down and go from there. It wasn’t a big deal, I think they liked “solving the puzzle” of which term to put where! (This is the second half of the page – the “multiplying using FOIL doesn’t” is from the last example.)

Some kids liked the Factoring By Grouping because it’s less to write down (that’s what they said), but when I walked around the class most of the kids were using the Generic Rectangle to factor the 4-term expressions.
That’s it. I wish I had known about the Generic Rectangle when I learned how to factor and multiply as a child. I wish I had known about it when I taught algebra for all those years, instead of teaching a different method for each type of expression. Seriously, for the basic ones like x^2 + 8x + 15 I’d tell the kids to set up their parentheses (x + )(x + ), leaving a blank space for the numbers and to “think about what multiplies to 15 and add to 8. If they needed help I’d set up the X (I had been shown how to do this, I didn’t connect it to anything, so didn’t connect it for the kids either, it was just a trick they could do), and put the 15 in the top and the 8 in the bottom – no 15x^2 or 8x, just the numbers. Then the kids would take the numbers on the side and fill them into their parentheses.
But if they had a problem with a leading coefficient that wasn’t 1, then I’d show them the “X-Box” method. But this time they’d have to remember that the top number in the X was really “a times c” (I did tell them this for the other type of problems, but since “a” was always 1, it didn’t wasn’t significant to them.) Then they’d have to make a box and put the “a” and “c” terms in diagonally, and the other boxes got the numbers from the sides of the X. Then they’d pull out the common terms and use them to fill in the parentheses of the factors, but sometimes make mistakes with the negatives and what went where. But since I just knew it as a trick, I didn’t tie it to multiplying the factors at all.
If they messed this up, then we would show them other ways to do it, like by making it 4 terms, using the sides of the X as the middle terms, and factoring out a GCF, or maybe just having them guess and check, because “the more they did, the better they’d get”. That’s how I learned it, right? And then I’d teach them another procedure to use when the problem had 4 terms – Factoring By Grouping.
But then I saw the Generic Rectangle method of factoring at a session at CMC, and it blew my mind. I remember coming back to my school and saying, “If we taught the kids to multiply the binomials this way, they could factor it with the Box and it would make sense! It wouldn’t be a trick!” My team didn’t want to change, so for a few years I didn’t either. But I eventually did!
And if this makes sense to you (hopefully it does) you can change how you teach it too.
But you need to buy in 100%, you can’t teach multiplying using FOIL, and factoring the simple problems with “think of what multiples to this and adds to that” or the X, and then pull out the Generic Rectangle for the “hard ones”. If you do this the Generic Rectangle will just be another procedure. It won’t flow. It won’t connect the multiplying with the dividing (AKA factoring). And the kids won’t see the beauty and connectivity of the algebra, they’ll just get frustrated trying to remember which procedure to use with each type of problem.
As Jo Boaler says, “Viva the Revolution!”

Wow – impressive. You just keep getting better and better! I understand why you wrote this blog – it was important to you to share this, because it’s so beautiful. Thanks for sending this to me, Love, Mom
>